Baseado Nos Exemplos Anteriores De M.M.C Resolva As Seguintes Deconposicoes, vamos embarcar numa jornada fascinante pelo mundo dos números! Aprenderemos a usar o mínimo múltiplo comum (MMC) para desvendar os segredos da decomposição numérica. Prepare-se para desvendar mistérios matemáticos, aplicando o MMC em situações práticas do dia a dia, de forma clara e descomplicada. Vamos lá, sem medo de errar, pois a prática leva à perfeição!
Este guia passo a passo vai te mostrar como o MMC facilita a resolução de problemas que parecem complexos à primeira vista. Através de exemplos práticos e bem explicados, você aprenderá a identificar os passos-chave na resolução de problemas com MMC, desde a decomposição em fatores primos até a aplicação em situações reais, como somar frações. Com a prática e dedicação, você dominará essa ferramenta matemática essencial.
Mínimo Múltiplo Comum (MMC): Uma Abordagem Prática: Baseado Nos Exemplos Anteriores De M.M.C Resolva As Seguintes Deconposicoes
O Mínimo Múltiplo Comum (MMC) é o menor número inteiro positivo que é múltiplo de dois ou mais números inteiros. Ele desempenha um papel crucial na resolução de diversos problemas matemáticos, especialmente aqueles envolvendo frações e problemas de divisão equitativa. Compreender o MMC facilita a solução de problemas do dia a dia, como dividir igualmente pizzas entre amigos ou determinar o tempo de encontro de ônibus que partem em horários diferentes.
Conceito e Importância do MMC
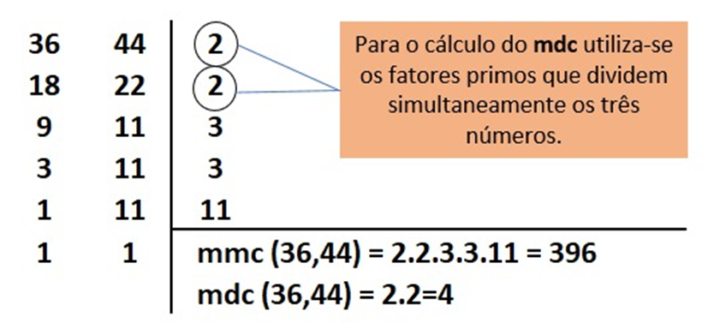
O MMC é fundamental para encontrar o menor múltiplo comum entre dois ou mais números. Sua importância se estende a diversas áreas, como na simplificação de frações, na resolução de problemas de proporcionalidade e na determinação do menor tempo comum em problemas de cronometragem.
Exemplos cotidianos incluem determinar a frequência de eventos que ocorrem em intervalos diferentes (como a coincidência de horários de ônibus), ou dividir igualmente recursos entre grupos de pessoas com quantidades diferentes.
Métodos de Cálculo do MMC
Existem vários métodos para calcular o MMC. A escolha do método depende da complexidade dos números envolvidos e da familiaridade com cada técnica. Abaixo, uma tabela comparativa de alguns métodos:
| Método | Descrição | Vantagens | Desvantagens |
|---|---|---|---|
| Fatoração | Decompor os números em seus fatores primos e multiplicar os fatores comuns e não comuns com o maior expoente. | Eficiente para números menores; fácil de visualizar a decomposição. | Pode ser trabalhoso para números grandes; requer conhecimento de fatoração prima. |
| Diagrama de Venn | Representar os fatores primos dos números em círculos de Venn e multiplicar os fatores presentes em qualquer círculo. | Visualmente intuitivo; ajuda a entender os fatores comuns e não comuns. | Menos eficiente para números grandes; pode ser confuso com muitos fatores. |
| Divisão sucessiva | Dividir os números sucessivamente por seus fatores primos até chegar ao número 1. O MMC é o produto de todos os divisores usados. | Eficiente para números de qualquer tamanho; processo sistemático. | Requer um pouco mais de organização do que a fatoração. |
| Máximo Divisor Comum (MDC) | Utilizar a relação entre MMC e MDC: MMC(a,b)
|
Eficiente se o MDC já for conhecido; utiliza uma relação matemática. | Requer o cálculo prévio do MDC. |
Exemplos de Problemas Resolvidos com MMC, Baseado Nos Exemplos Anteriores De M.M.C Resolva As Seguintes Deconposicoes

A seguir, três exemplos ilustram a aplicação do MMC na resolução de problemas:
- Exemplo 1: Encontrar o menor tempo em que três lâmpadas, que piscam a cada 2, 3 e 4 segundos, respectivamente, piscam simultaneamente. (MMC(2, 3, 4) = 12 segundos)
- Exemplo 2: Determinar o menor número de doces que podem ser divididos igualmente entre 6, 8 e 12 crianças, sem sobrar nenhum doce. (MMC(6, 8, 12) = 24 doces)
- Exemplo 3: Encontrar o menor número que, ao ser dividido por 5, 7 e 11, deixa resto 2 em cada divisão. (Este problema requer um pouco mais de raciocínio, envolvendo o MMC e o resto da divisão.)
Em cada exemplo, os passos cruciais envolvem identificar os números relevantes, calcular o MMC utilizando o método mais apropriado e interpretar o resultado no contexto do problema.
Decomposição Numérica com MMC
O MMC auxilia na decomposição de números em seus fatores primos, embora não seja o método mais direto. A fatoração prima é geralmente mais eficiente. No entanto, o conhecimento do MMC pode ser útil em alguns casos para entender a composição dos números.
| Número | Fatores Primos | Decomposição | Observações |
|---|---|---|---|
| 12 | 2, 3 | 2² x 3 | |
| 18 | 2, 3 | 2 x 3² | |
| 24 | 2, 3 | 2³ x 3 |
Comparando as decomposições, observamos os fatores primos comuns (2 e 3) e seus diferentes expoentes.
Resolução de Problemas com Base nos Exemplos Anteriores

Vamos resolver alguns problemas utilizando o MMC:
- MMC de 15, 20 e 30: Fatorando os números: 15 = 3 x 5; 20 = 2² x 5; 30 = 2 x 3 x 5. O MMC(15, 20, 30) = 2² x 3 x 5 = 60.
- Menor número divisível por 6, 8 e 12: MMC(6, 8, 12) = 24.
- Problema prático: Três amigos correm em uma pista circular. O primeiro completa uma volta a cada 10 minutos, o segundo a cada 12 minutos e o terceiro a cada 15 minutos. Em quanto tempo eles se encontrarão novamente no ponto de partida? MMC(10, 12, 15) = 60 minutos.
Eles se encontrarão novamente no ponto de partida após 60 minutos.
Extensão do Conceito de MMC
O MMC é essencial para somar e subtrair frações. Para somar frações com denominadores diferentes, é necessário encontrar o MMC dos denominadores para obter um denominador comum.
Exemplo: Somar 1/4 + 2/3. O MMC(4, 3) = 12. Então, 1/4 = 3/12 e 2/3 = 8/12. Portanto, 1/4 + 2/3 = 3/12 + 8/12 = 11/12.
Um método alternativo para calcular o MMC é usar a fatoração prima repetida, que é especialmente útil para números grandes.
O MMC e o Máximo Divisor Comum (MDC) são conceitos inversamente relacionados. O produto do MMC e do MDC de dois números é igual ao produto dos dois números.

